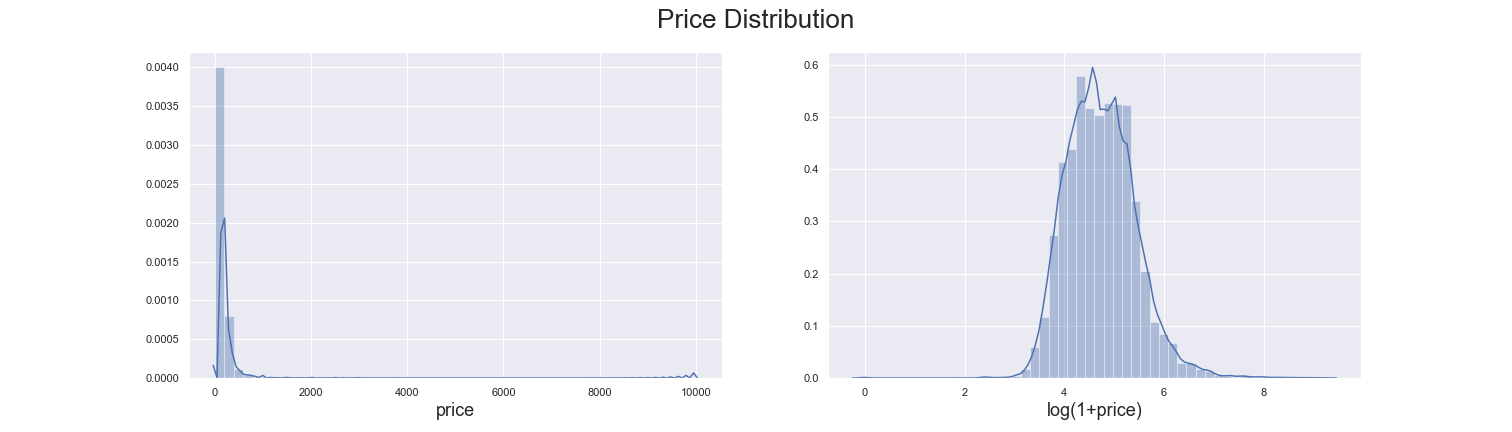
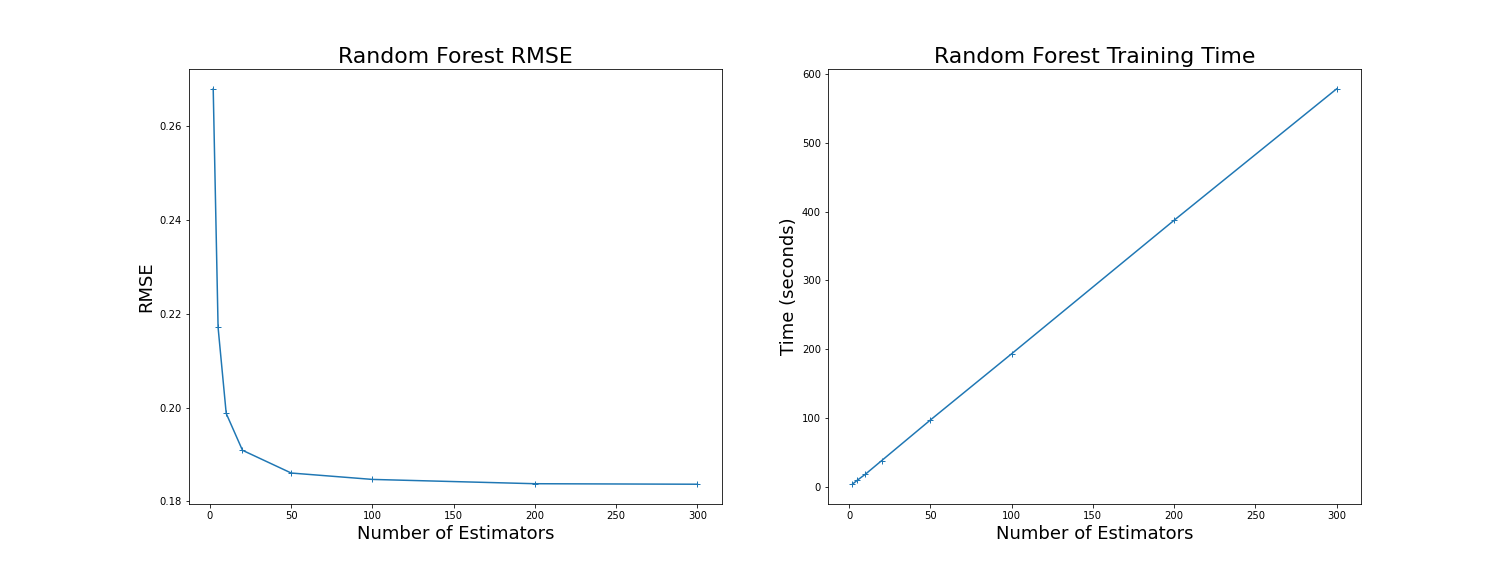
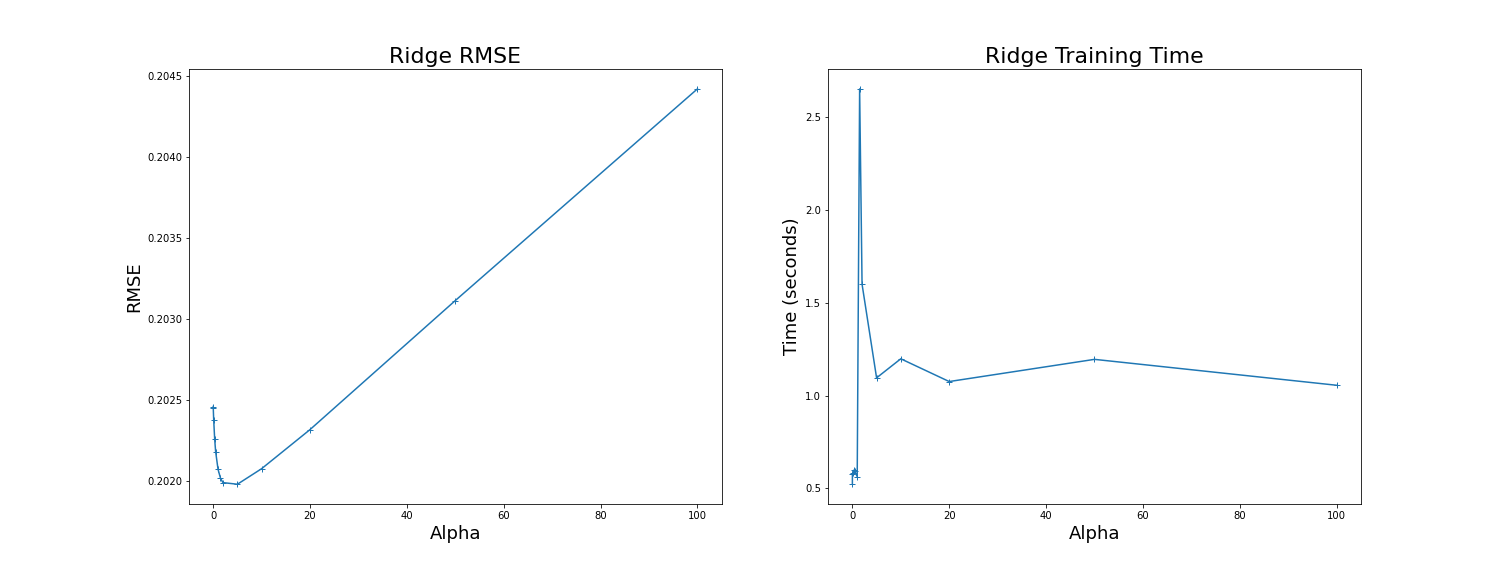
Data Visualization
We can visualize the data in various ways to attempt to understand it. Below, we visualize the price distribution in each borough or neighbourhood group to see the relationship between prices and borough. This figure shows that while
all boroughs have expensive properties, some, like Queens and Bronx, have a larger portions of cheaper properties. Contrarily, Manhattan seems to have higher portions of more expensive properties.
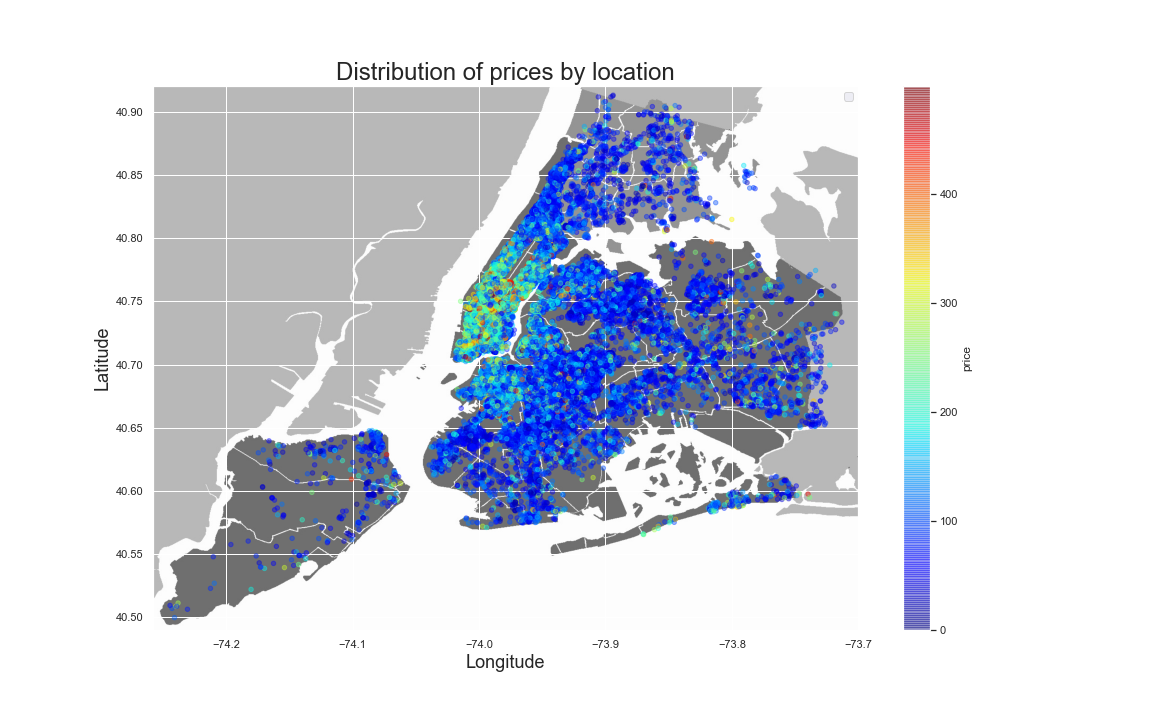
This figure also shows that the neighbourhood group is an important feature for the model that can help it estimate an ideal price for the listing. Another important feature is the specific location or coordinates of the listing. As
shown by the first figure on the right, the location of the listing impacts it's price; as such, certain areas have a higher concentration of expensive listings.
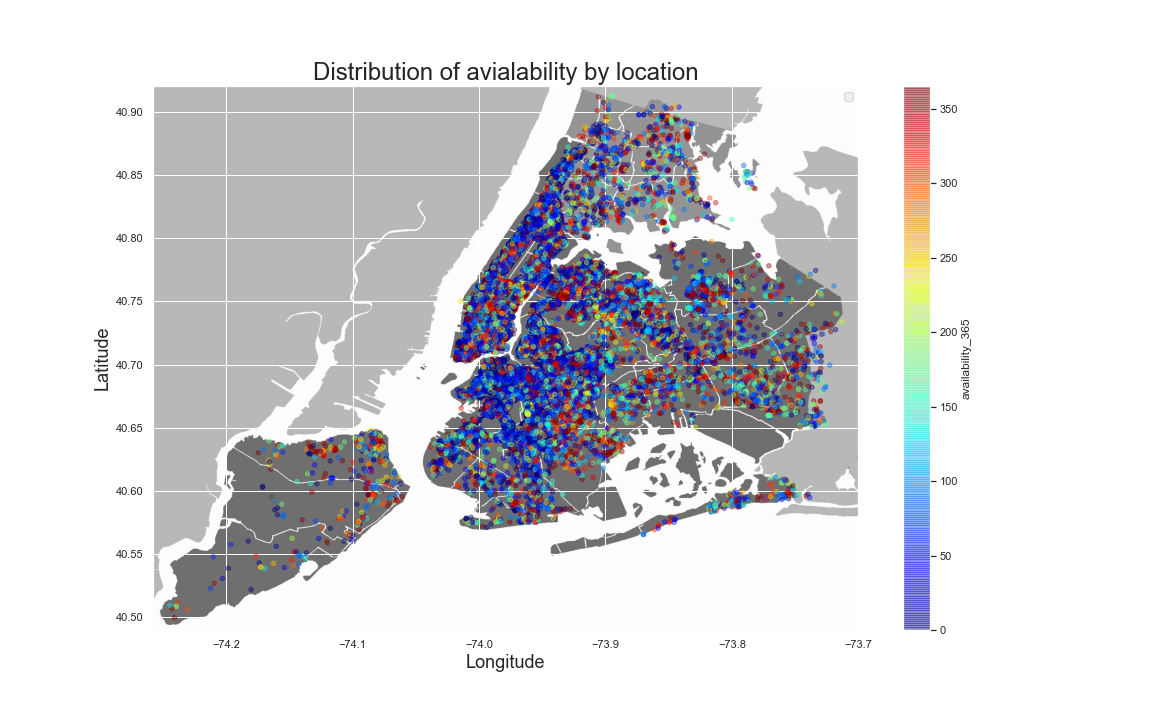
Another attribute that can be visualized is the availability accross the map. This is shown in the second figure on the right.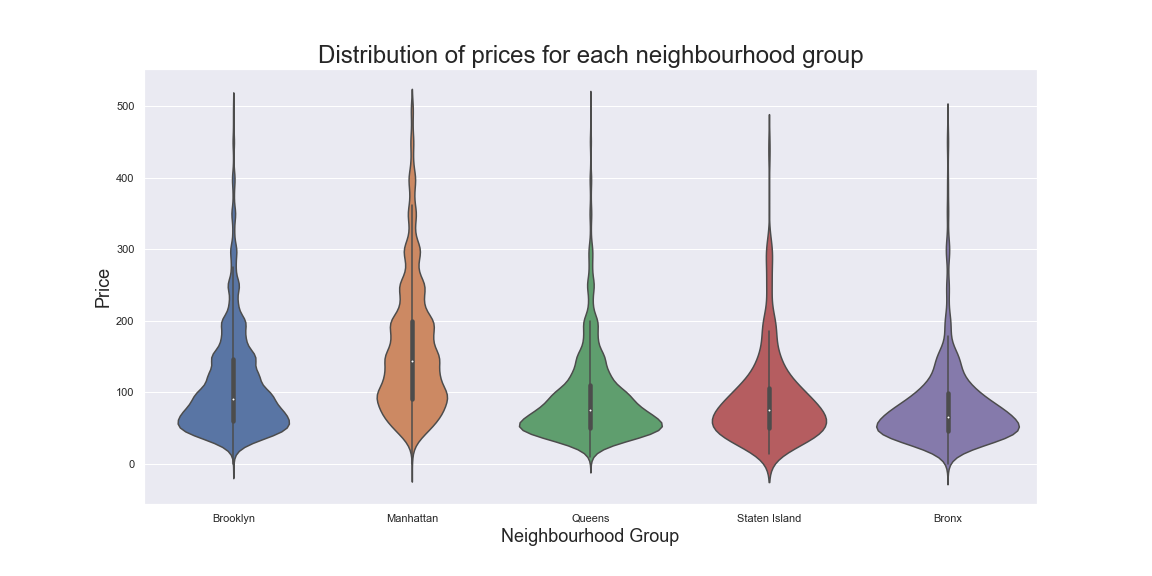
Another attribute that can be visualized is the availability accross the map. This is shown in the second figure on the right.